Em meados do século IXX George Boole desenvolveu um sistema matemático de análise lógica. Sistema este conhecido como Álgebra de Boole . Esta álgebra trabalha apenas com valores 0 e 1.

A álgebra de Boole só começou a ter importância na eletrônica depois do desenvolvimento do transistor , estes transistores são a base de dispositivos eletrônicos diminutos chamados portas lógicas.

Eis as portas lógicas abaixo com as respectivas tabelas verdade:

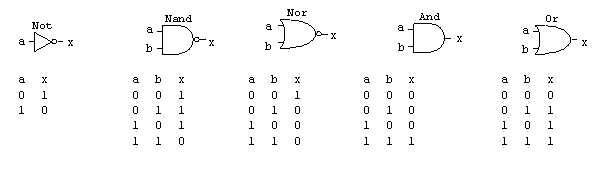
As portas universais são Nand e Nor em virtude de necessitarem de apenas 2 transistores para construí-las.

Postulados De Boole

1) 0 + A = A
2) 1 + A = 1
3) A + A = A
4) A + A = 1
5) 0 . A = 0
6) 1 . A = A
7) A . A = A
8) A . A = 0
9) A = A
10) A +B = B + A Propriedade Comutativa
11) A . B = B . A
12) A + (B + C) = (A + B) + C = A + B + C Propriedade Associativa
13) A (B . C) = (A . B) C = A . B . C
14) A (B +C)= A .B + A . C Propriedade Distributiva
15) A + A . B = A
15.a) A + B .C = (A + B) (A + C)
16) A (A + B) = A
17) (A + B) (A + C) = A + B . C
18) A + B A = A + B
18.a) A ( A + B) = A . B
19) A . B + A . B = A
20) (A + B) (A + B ) = A
21) A . B + A . C = (A + C) ( A + B)
22) (A + B) ( A + C) = A .C + A C
23) A . B + A . C + B .C = AB + A C
24) (A + B) ( A + C) (B + C) = (A + B) ( A + C)

Estes postulados nos ajudam a simplificar funções; mas existe uma ferramenta muito mais potente chamada Mapa de Karnaugh.

Equivalência de circuitos

Voltar